Complexity

Timing Our Code

同一個函數，我們會有好幾種不同的實做方式，那要如何去比較哪一個實做是最佳的呢？一個較為直觀的方式是直接比較不同函數的執行時間。

在 JavaScript 中，我們可以在調用函數前後使用 performance.now() 來取得當前的時間，藉由計算兩者的差值來獲得函數運行的時間：

// Solution 1
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }

  return total;
}

// Solution 2
function addUpTo(n) {
  return (n * (n + 1)) / 2;
}

let time1 = performance.now();
addUpTo(100);
let time2 = performance.now();
console.log(`Time Elapsed: ${(time2 - time1) / 1000} seconds.`);

然而使用函數的運行時間來判斷效能，有其侷限性：

• 對於速度較快的演算法來說，不容易獲取到精確的運行時間
• 不同的機器，由於硬體配置狀況不一樣，函數的運行時間也就不一樣
• 同一台機器，由於運行函數當下的記憶體和系統狀況不一樣，在不同時間點所得到的結果也不一致

Counting Operations

換個方式，我們還可以計算函數運行的過程中，進行了多少次的賦值、四則運算…等的「基本操作」：

// 3 simple operations
function addUpTo(n) {
  return (n * (n + 1)) / 2;
}

// n simple operations
function addUpTo(n) {
  let total = 0;
  for (let i = 1; i <= n; i++) {
    total += i;
  }
  return total;
}

Big O Notation

Time Complexity

在計算機科學中，我們使用時間複雜度（Time Complexity）來描述一個演算法的執行時間，在 Performance Tracker 中，提供了時間複雜度的視覺化圖表，可以顯示運行時間和輸入規模的關係圖。

我們通常會以大 O 記號（Big O Notation）來表示一個演算法的時間複雜度。如果說一個演算法是 $O(g(n))$ 的時間複雜度，代表這個演算法的基本操作次數 $f(n)$ 隨著輸入規模 $n$ 的增長，最終會以 $cg(n)$ 為上界（Upper Bound）：

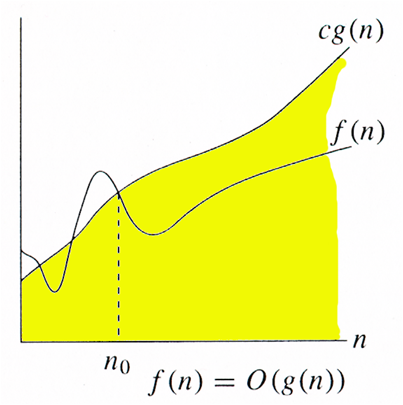
其中常見的 $g(n)$ 可以是:

• 線性（Linear）: $g(n) = n$
• 平方（Quadratic）: $g(n) = n^2$
• 常數（Constant）: $g(n) = 1$
• ...

Simplifying Big O Expressions

對於估算時間複雜度，有以下規則可以用來簡化 Big O Notation 的表示方式：

1. 乘法常數係數可忽略
   • $O(2n) \rightarrow O(n)$
   • $O(500) \rightarrow O(1)$
   • $O(13n^2) \rightarrow O(n^2)$
2. 較小的次方項可忽略
   • $O(n + 10) \rightarrow O(n)$
   • $O(1000n + 50) \rightarrow O(n)$
   • $O(n^2 + 5n + 8) \rightarrow O(n^2)$

除此之外，在 JavaScript 中：

• 算術運算為 $O(1)$
• 變數賦值為 $O(1)$
• 透過索引存取陣列為 $O(1)$
• 透過鍵值存取物件為 $O(1)$

Space Complexity

除了時間複雜度之外，Big O Notation 也能夠用來描述空間複雜度（Space Complexity），實際上一個演算法所使用到的空間包含了輸入資料的儲存空間和運算時額外或用來暫時存儲的輔助空間（auxiliary space）。

如果沒有特別標明的話，一般談論的空間複雜度指的就是輔助空間複雜度（auxiliary space complexity）。

在 JavaScript 中要考慮空間複雜度時：

• 基本類型（Primitive Types）
  • boolean、number、undefine 和 null 為 $O(1)$
  • 字串長度 $n$ 的 string 為 $O(n)$
• 參考類型（reference type）
  • 陣列大小 $n$ 的 array 為 $O(n)$
  • 鍵值數目 $n$ 的object 為 $O(n)$