# Building a Strong Foundation

# What is STL?

C 語言和 C++ 語言之間有個巨大的差異在於後者提供了 標準模板庫（STL, Standard Template Library）。在 C++ 標準模板庫中提供了一系列的模板可以使代碼更加簡潔俐落，透過 #include <bits/stdc++.h> 來引入。

# Sort

// Without STL
void MergeSort(int st, int dr) {
  if (st < dr) {
    int m = st + rand () % (dr - st + 1);

    MergeSort(st, m);
    MergeSort(m + 1, dr);

    int i = st, j = m + 1, k = 0;

    while (i <= m && j <= dr)
      if (v[i] < v[j]) tmp[++k] = v[i++];
      else tmp[++k] = v[j++];

    while (i <= m)   tmp[++k] = v[i++];
    while (j <= dr)  tmp[++k] = v[j++];

    for (i = st, j = 1; i <= dr; i++, j++)
      v[i] = tmp[j];
  }
}

// With STL
sort(a+1, a+n+1);

# Swaping

// Without STL
aux = a;
a = b;
b = aux;

// With STL
swap(a, b);

# Max

// Without STL
if (a > b) maximum = a;
      else maximum = b;

// With STL
maximum = max(a, b);

# How to Prepare for Competitive Programming?

講師撰寫了一篇文章 How to prepare for competitive programming? 來說明自己怎麼準備程式競賽的，其中大致上提到了幾點：

選擇一門適當的程式語言。因為 STL 有效地簡化開發過程，這部分極為建議採用 C++ 作為主力語言；而 Java 運行速度較慢可能超出題目的時間限制。
透過 Online Judge 網站進行練習，這裡建議可以使用 Sphere Online Judge (SPOJ)，至少先解完裡面的前 250 道題。
找到屬於自己的代碼風格，這將有利於開發、調試與閱讀。
熟練經典的資料結構與演算法，推薦的資源：
刻意並持續地練習，在作者準備程式競賽的八個月中，每天至少練習五個小時以上。

# Algorithms Complexity

一個程序的運行時間通常會取決處理器的核心數目、記憶體的讀寫速度、作業系統的位元數和輸入的資料數量…等。通常會使用 大 O 記號（The Big O Notation） 來表示時間複雜度，如果要以此記號方式來表示程式運行的時間複雜度，有一些原則必須遵守：

捨棄較小的次方項。
捨棄常數項的乘法係數。

# Appearance Array

如果給定一個數列，如何判斷某個數字是否在數列中存在？數字在數列中重複了幾次？我們可以創建 Appearance Array：

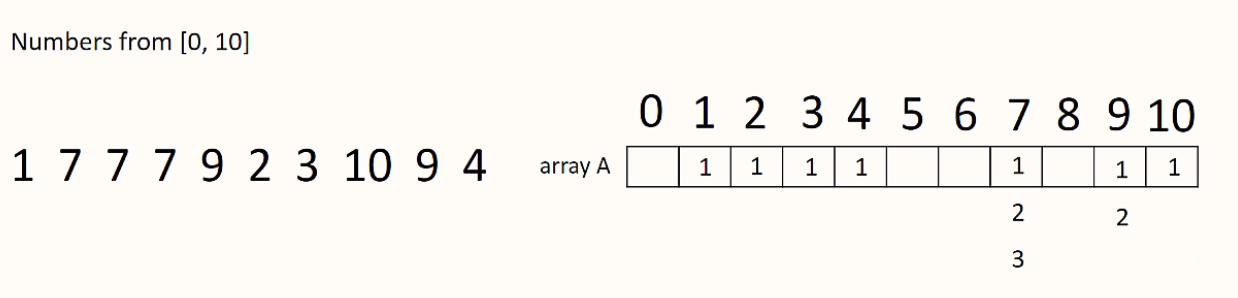
如上圖所示，若已知數字的範圍，可以建立一個大小與數字範圍相等的陣列，逐一讀取數列中的數字，並存取對應的陣列索引值。若數列中的數字共有 $n$ 個，則這個做法的時間複雜度為 $O(n)$ 。再更深入一些，倘若今天數列中的數字包含負整數呢？由於陣列的索引值不可能為負，所以我們必須進行平移的動作，假設今天數列中最小的數字為 -10，則以索引 0 的位置表示 -10 即可。

# [Note] Counting Sort

計數排序（Counting Sort）是一種穩定的線性時間排序演算法，計數排序使用 Appearance Array 來記錄元素出現的次數，此陣列 A[i] 的第 i 個元素是待排序陣列中數值等於索引值 i 的元素的個數。演算法的步驟如下：

找出待排序陣列中最大和最小的元素
循序累計陣列中每個值為 i 的元素出現的次數，並存入計數陣列中的第 i 項
對所有的計數進行累加（從計數陣列中的第一個元素開始，每一項和前一項相加）
反向填充目標陣列：將每個元素 i 放在新陣列的第 i 項，每放一個元素就將 i 的數值減去 1。

# [Note] Check Parenthesis Expression

由左至右讀入陣列
遇到左括號 [ ( { 時，推入堆疊中
遇到右括號 ] ] } 時，彈出堆疊頂部元素
若最後堆疊為空，表示括號成對

# [Note] How to Prepare for the Coding Interview?

講師寫了一篇文章 The definitive guide to the coding interview 說明如何準備軟體面試。

其中最重要的一條就是「There is no such shortcut or trick to pass the interview. The single way to find optimal solutions to algorithmic problems is by practicing, solving as many problems as possible. In short, it’s hard work.」

而在面試過程中，對於資料結構和演算法的問題是無法避免的，常見必須要掌握的知識點總結如下：

Big O Notation: 我們透過時間複雜度來評估一個演算法的好與壞，因此必須了解它的含意。
陣列（array）: 必須熟悉基礎的陣列概念，通常問題會涉及元素的存取，比如透過兩個指針來進行迭代；除此之外，一個經典的問題是檢查一個給定的數組是否有序。
字串（string）: 在常用的程式語言中瞭解他如何操作字串，通常考察的點會是連接或是旋轉字串…等問題。
鏈接列表（linked list）: 鏈結列表經常考察極端的條件狀況，如果鏈表為空會發生什麼？如果只有一個元素的鏈表會如何？如果想要迭代直到最後一個元素？
雜湊表（hash table）: 雜湊表在大多數的面試中也會被問到，必須要熟悉自己選擇的程式語言中的雜湊表庫；試著練習如何求解最大子數列問題。
堆疊（stack）: 堆疊只能在一端進行操作；試著使用堆疊實作查找最大值的功能。
貯列（queue）: 貯列存在兩端，不要將與堆疊混淆；試著使用兩個堆疊實作一個貯列。
貪心（greedy algorithm）: 貪心演算法指在特定時刻做出最佳決策而不考慮未來的後果，在這樣的前提下得到的結果未必永遠都是全局的最優值。
原始類型（primitive types）: 主要涉及位元操作和數字基本運算；嘗試計算二進制表示中 1 的數量。
二元樹（binary tree）: 如何走訪遍歷二元樹十分重要，涉及如何找到所有子節點的共同祖先並進行遞歸遍歷。
堆（heap）: 堆被廣泛用於現實世界的應用程式；練習直到你可以確信何時要使用最小堆或最大堆？如何打印數列中最大的五個元素？使用最小堆還是最大堆？
搜索（search）: 搜索演算法也是經常被使用到的核心主題，建議使用二元搜索至少練習幾個問題。
排序（sorting）: 確保自己可以實作出合併排序（Merge Sort）和快速排序（Quick Sort）；並區分不同排序演算法的最優、平均和最糟狀況下的複雜度。如果有額外的時間，可以學習堆排序（Heap Sort）。
二元搜索樹（binary search tree）: 需要能夠實現所有基本操作，包括刪除元素！
回溯（backtracking）: 當題目要求要生成所有可能的解決方案並採取符合要求的解決方案時經常使用；嘗試實現集合的冪集和皇后問題。
圖（graph）: 圖可能是計算機科學中最常被使用的資料結構，不論是社交網路、路徑規劃…等都是一個巨大的圖；在這一個單元中，必須熟悉如何在記憶體中實作圖的結構，以及檢查一個圖是否有環。
動態規劃（dynamic programming）: 動態規劃也是一個需要被掌握的能力，它其實更傾向於一種解決問題的拆分思路，而不是一個有著實際步驟的解法。

在文章的後半部，作者模擬了當他實際在面試現場被問到問題時，該如何去拆解與回答，十分建議可以看一下影片中的內容。

# [Note] Binary Search

使用二分搜索演算法在一個已排序的陣列中查找指定的數值時，複雜度是 $O(\log(n))$ ，二分搜索每次搜索時先從陣列中間的元素開始查找，根據比較所得的結果來丟棄不必要的部分，反覆更新查找範圍直至找到元素或無法找到元素為止。

← Getting Started Dynamic Programming →