# Q-Learning Intuition

# What is Reinforcement Learning?

強化學習（RL, Reinforcement Learning）是機器學習中的一個領域，強調如何基於環境（Environment）而行動（Action），以取得最大化的預期利益。一個基本的強化學習模型由環境（Environment）、智能體（Agent）、動作（Action）和獎勵（Reward）所構成，如下圖所示：

What is Reinforcement Learning?

強化學習不需要透過標記資料，而是透過獎勵訊號來影響後續收到的資料來進行學習，值得一提的是獎勵訊號不一定是實時的，而是可以延後出現，因此在強化學習中，經常需要處理時間序列。

# The Bellman Equation

貝爾曼方程式（The Bellman Equation）又稱為動態規劃方程式（Dynamic Programming Equation），是用來描述動態規劃問題能夠達到最佳化的必要條件。在不涉及變化的確定環境中，這個方程式將決策問題在特定狀態的值表示成如下形式：

V(s) = \max_a{(R(s, a) + \gamma V(s'))}

其中：

$V(s)$ 表示決策問題在特定狀態 $s$ 的值
$V(s')$ 延伸決策問題的值
$R(s, a)$ 執行動作所得到的報酬
$\gamma$ 為折扣因子，距離報酬越遠的影響越小

由於對於每一個智能體來說，在每一個狀態下可以採取的行動 $a$ 不只一個，所以 $V(s)$ 要取最大值。

# Example: The Maze

# The Simple Way to Mark State Value

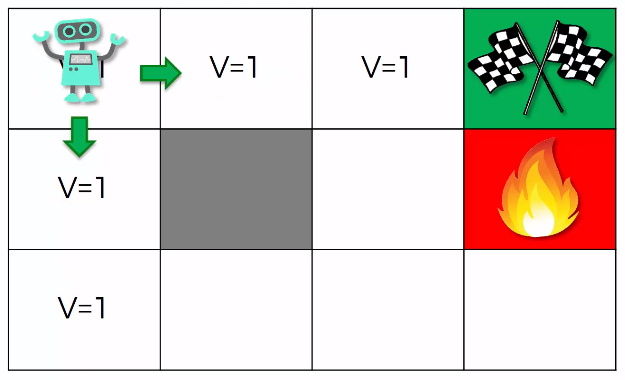
Simple Way

在上述的圖片中有一個簡易的迷宮，一共有 $3 \times 4 = 12$ 個狀態，我們要決定如何行走到綠色旗幟的位置，我們將該位置的報酬設定為 $1$ ，而紅色火堆處的報酬則設定為 $-1$ 。

首先我們考慮一個簡單的狀況：「將特定狀態的值，設定為執行動作所能得到的最大報酬」，在這樣的前提下，我們不難得到上圖的結果。然而此時有一個問題…如果我們的起始位置在左上角的話，此時我該向下走呢？還是向右走？

# Use The Bellman Equation to Mark State Value

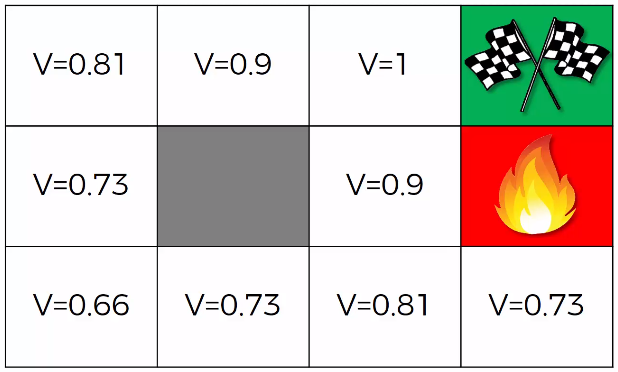
Use The Bellman Equation

現在我們假定折扣因子為 $0.9$ 並使用貝爾曼方程式來計算每一個狀態的 $V(s)$ 如上圖所示，如此一來便解決了前面遇到的問題。

# Markov Decision Processes (MDPs)

# Deterministic Search and Non-Deterministic Search

Deterministic Search and Non-Deterministic Search

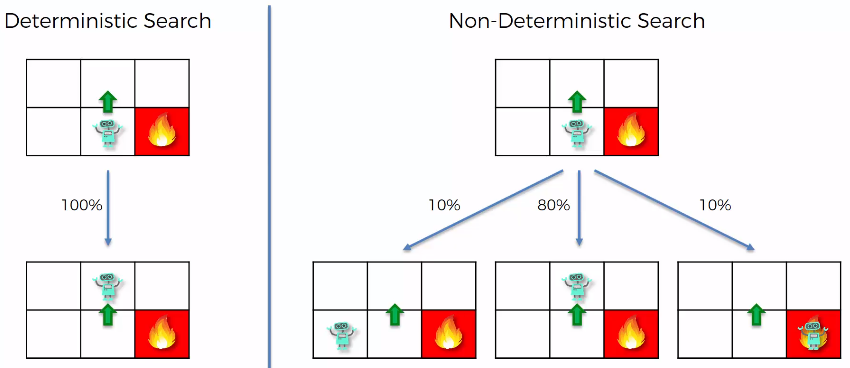
真實世界中的環境通常都會存在隨機性，我們無法知道採取了某個行動之後，就會產生怎樣的結果。比如當我們的智能體決定要往上走時，有可能：

$80\%$ 的機率會走到上面那格
$10\%$ 的機率會走到左邊那格
$10\%$ 的機率會走到右邊那格

這樣的問題稱為非決定性搜索問題（non-deterministic Search Problem），當我們遇到這樣的問題時，就需要引入馬可夫決策過程（MDPs, Markov Decision Processes）來進行描述。

# Markov Decision Processes (MDPs)

如果說系統的下一個狀態只與當前狀態有關，而與更早之前的狀態無關，我們就說這個系統具有馬可夫性質（Markov Property）。當我們的學習模型，其環境的系統狀態具有馬可夫性質時，就可以透過馬可夫決策過程（MDPs, Markov Decision Processes）來進行描述與建模，可以簡單表示為：

M = (S, A, P_{sa}, R, \gamma)

其中：

$S$ 表示狀態集合
$A$ 表示動作集合
$𝑃_{sa}$ 表示當前狀態 $s$ 經過動作 $a$ 後，轉移到其他狀態的機率分佈情況。比如 $P(s'|s, a)$
$R$ 表示報酬函數（reward function）
$\gamma$ 為折扣因子，距離報酬越遠的影響越小

基於隨機性，我們將狀態轉移機率納入上述的貝爾曼方程式（The Bellman Equation）可以得到：

V(s) = \max_a{\left(R(s, a) + \gamma \sum_{s'} P(s, a, s') V(s')\right)}

# Living Penalty

直到目前為止，我們的獎勵只出現在終點；實際上，我們可以在每一次狀態改變時都給予獎勵，比如說在每一次狀態改變時都添加 $R(s)=-0.04$ 的獎勵，這樣一來可以減少行走的次數，但是獎勵值的選取也是一個問題。

如下圖所示，當 $R(s)=-2$ 時，由於比起最終結束的 $R=-1$ 要更小，所以可以看到下圖的結果會導致智能體想要儘快結束而選擇直接往紅色火堆處移動的決策：

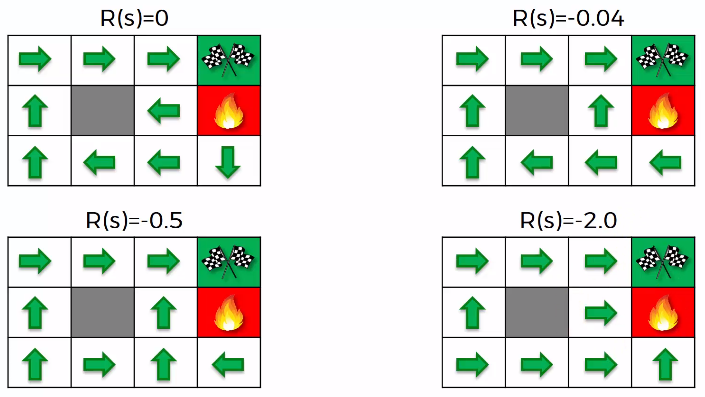
Living Penalty

# Q-Learning

Q(s, a) = R(s, a) + \gamma \sum_{s'} \left(P(s, a, s') \max_{a'} Q(s', a') \right)

# Temporal Difference

← Introduction Artificial Neural Networks →